[심층신경망2] 이론
1. neural network(NN)을 이용한 XOP문제의 해결
-> 레이어를 여러개 쌓아서 해결(2개이상)
2. Deep Neural Network(DNN)을 통한 어려운 문제 도전-> 깊게 쌓았더니 학습이 잘 이루어지지 않는 문제 발생
3. DNN에서 Gradient Vanishing문제 발생 (DNN이 제 기능을 하지 못함)
Geoffrey Hinton's summary of finding up to today-> DNN에서 Gradient Vanishing문제 해결법
-out labeled datasets were thousands of time too small
-out computers were millions of times foo slow
-🌞we initialized the weights in a stupid way (좋지 않은 weight 초기화 방법을 사용하고 있었음)
-🌞 we used the wrong type of non-linearity (잘못된 활성함수 사용)
Activation Function-활성함수
활성화함수는 신경학적으로 볼 때 뉴런 발사(Firing of Neuron)의 과정에 해당함
최종 출력 신호를 다음 뉴런으로 보내줄지 말지 결정하는 역할을 함

-뉴런이 다음 뉴런으로 신호를 보낼 때 입력신호가 일정수준 이상이면 보내고 기준에 달하지 못하면 보내지 않을 수도 있음. 즉, 활성 함수란 그 신호를 결정해주는것
-많은 종류의 활성화 함수가 있고, Activation function의 결정이 결과에 크게 영향을 미침
1. Step
입력이 양수일때 1, 음수일때 0의 신호를 보내주는 이진함수
미분 불가능한 함수로 모델 Optimization과정에 사용이 어려워 신경망의 활성함수로 사용하지 않음
(활성함수로 쓸 수 있다는 의미= "미분이 가능하다" - 왜냐하면 back propagation이라는 과정이 결국 weight를 갱신할 때 각 노드 위치에서의 편미분 값을 활용하게 되는데 그 미분이 불간으하기 때문)
Gradient update과정을 통해서 weight를 갱신하고 있는 신경망 구조를 사용하고 있는 상태에서는 더이상 step function을 신경망의 활성함수로 사용할 수 없게 됨
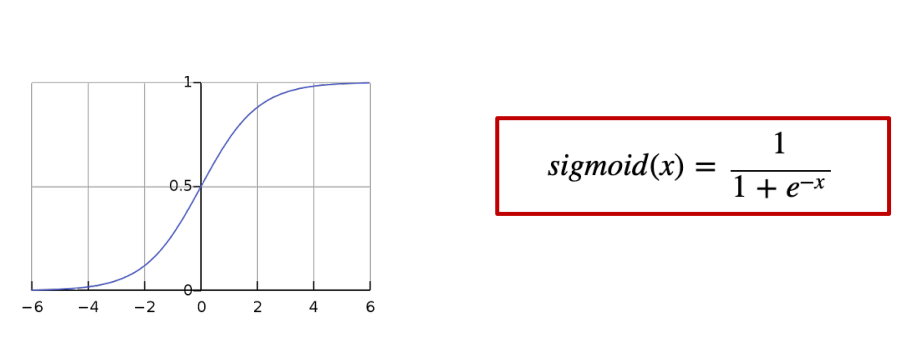
2. Sigmoid
단일 퍼셉트론(perceptron)에서 사용했던 활성함수
입력을 (0,1)사이로 정규화함
Backpropagation단계에서 NN layer를 거칠 때마다 작은 미분 값이 곱해서, Gradient Vanishing을 야기함. 여러개의 layer를 쌓으면 신경망 학습이 잘 되지 않는 원인
Deep Layer(3개이상)에서 활성함수로 사용을 권하지 않음
2. tanh
sigmoid를 보완하고자 제안된 활성함수
입력을 (-1,1)사이의 값으로 정규화함
sigmoid보다 tanh함수가 전반적으로 성능이 좋음
여전히 Gradient Vanishing문제는 발생함(sigmoid보다는 덜 발생)

3. ReLU(Rectified Linear Unit)
현재 가장 인기있는 활성화 함수
양수에서 Linear Function과 같으며 음수는 0을 출력하는 함수
미분값을 0또는 1의 값을 가지기 때문에 Gradient Vanishing 문제가 발생하지 않음
Linear Function과 같은 문제는 발생하지 않으며, 엄연히 Non-Linear함수이므로 Layer를 deep하게 쌓을 수 있음
exp()함수를 실행하지 않아 sigmoid나 tanh함수보다 6배 정도 빠르게 학습이 진행됨

4. Leaky ReLU
Leaky ReLU는 'dying ReLU'(: 0보다 작은 구간을 모두 0으로 출력) 현상을 해결하기 위해 제시된 함수
ReLU는 x<0인 경우 함수 값이 0이지만, Leaky ReLU는 작은 기울기를 부여함
보통 작은 기울기는 0.01을 사용
Leaky ReLU로 성능향상이 발생했다는 보고가 있으나 항상 그렇지는 않음

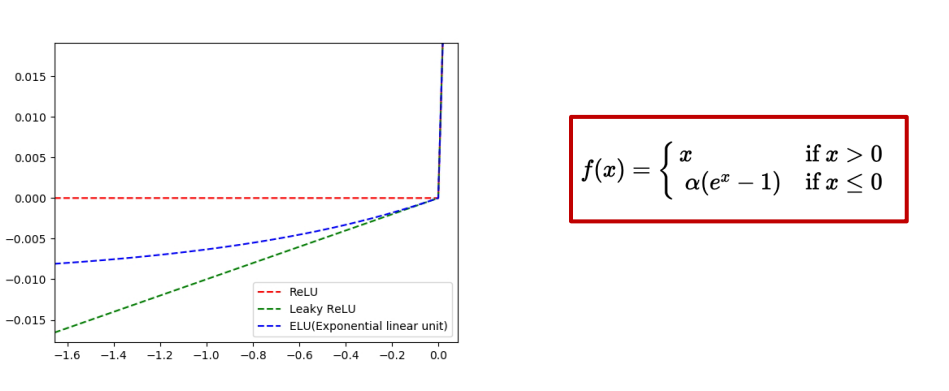
5. ELU(Exponential Linear Units)
ReLU의 threshold를 -1로 낮춘 함수를 exp^(x)를 이용하여 근사한것
dying ReLU 문제를 해결함
출력값이 거의 zero-centered에 가까움(layer를 통과했을 때 나온 출력 자체도 정규화 되어있음)
하지만 ReLU, Leaky ReLU와 달리 exp()를 계산해야하는 비용이 듦
6. Maxout
ReLU와 Leaky ReLU를 일반화 한것. ReLU와 Leaky ReLU는 이 함수의 특수한 경우
Maxout은 ReLU가 갖고있는 장점을 모두 가지며, dying ReLU문제도 해결
ReLU함수와 달리 한 뉴런에 대해 파라미터가 두배이기 때문에 전체 파라미터가 증가한다는 단점이 있음 ->연산량이 증가하지는 않음(exp형태 x) 파라미터를 저장하기 위한 메모리 자원은 증가

정리: Maxout > ELU, Leaky ReLU >= ReLU > tanh >= sigmoid
가장먼저 ReLU를 시도 : 현재까지 가장 많이 사용되는것
다음으로 Leaky ReLU, Maxout, ELU를 시도(성능이 좋아질 수 있는 가능성이 있음/ 반드시 좋아지는 것은 아님)
tanh를 사용해도 되지만 성능이 개선될 확률이 적음
앞으로 Deep NN에서는 sigmoid는 피한다

Weight Initialization-> 똑똑한 방법으로 초기화
결과가 매번 상이할 수 있음=random initial을 사용하기 때문
random seed에 의해서도 학습의 경향성이 달라질 수 있음
기본적인 선형회귀나 softmax같은 알고리즘에서는 -1~1의 난수를 Weight로 사용
Neual Network에서는 weight 선정에 주의 요망
w=0이면 Backpropagation시 gradinet 값이 0이 되어 Gradient Vanishing현상이 발생(W가 0이 되면 갱신이 불가)
Need to set the initial weight values wisely
절대 모두 0으로 초기화히지 말것
가중치를 어떻게 초기화 할 것이냐는 무척 도전적인 이슈
Hinton et al. (2006) "A Fast LearningAlgorithm for Deep Belief Nets”
Restricted Boatman Machine (RBM)을 이용한 초기화 제안
RBM은 너무 복잡도가 높음
Simple methods ard OK : 노드의 입출력 수에 비례하여 초기값을 결정짓는 방법 제안(노드가 w,b값을 가지고 있는데 노드에 유입되는 입력의 수와 출력의 수로 w,b값을 초기화)
Makes sure the weights are ‘just right’, not too small, not too big
Using number of input (fan_in) and output (fan_out)
-Xavier initialization : torch.nn.xavier_nomal_

-He's initialization :torch.nn.kaiming_normal_

초기화 방법은 여전히 연구중
Drop and model Ensemble
overfitting :너무 과도하게 데이터에 대해 모델을 learning한 경우를 의미
현 학습 데이터만 잘 표현하면, 새로운 데이터에 대한 대응력이 없어 모델 학습 의미 상실


overfitting막는방법 : 학습 데이터 수 늘리기/ feature의 수 줄이기/ regularization:loss를 디자인 할때 W에 제약을 걸어 control(-dropout: 깊은 신경망(DNN을 만드는데 있어서 큰 공)
Dropout for overfitting
훈련 데이터에 대한 복잡한 공동 적응을 방지하여 신경망의 과적합을 줄이기 위한 Google이 제안한 정규화 기술
'드롭아웃'이라는 용어는 신경망에서 유닛을 제거하는 것
학습시에만 적용하고 테스트시에는 모든 유닛을 사용함

왜 성능 향상을 가져오는가?
드랍아웃을 통해 ensemble model학습과 같은 효과가 있기 때문
Ensemble model이란 집단 지성으로 이해할 수 있음! : (통계학과 기계 학습에서) 앙상블 학습법은 학습 알고리즘들을 따로 쓰는 경우에 비해 더 좋은 예측 성능을 얻기 위해 다수의 학습 알고리즘을 사용하는 방법을 말함
정리
-DNN 모델 학습을 위한 팁
--활성함수를 잘 선택한다(ReLU)
--가중치 초기화 방법을 잘 선택한다(Xavier가 가장 널리 사용)
--드랍 아웃을 잘 적용한다(NN-ReLU-Dropout 을 하나의 블락으로 쌓는다
--BN을 잘 적용한다(NN-ReLU-BN을 하나의 블락으로 쌓는다)